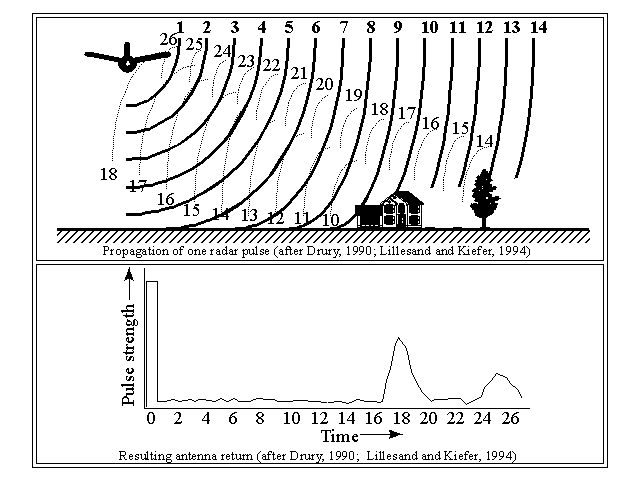
In a typical SLAR system, pulses of microwaves, at "bursts" of, typically, 0.000001 second are transmitted from the airborne source. The transmitter acts also as the receiver of reflected energy. The system records the amount of time it takes for the energy to make the round-trip from the instrument to the ground, and is then divided by 2 (since it is a round trip). The slant range (SR), or distance between the transmitter and the object, is calculated according to the equation:
SR=ct ÷ 2, where:
The detail or resolution of a radar system is dependent on two parameters:
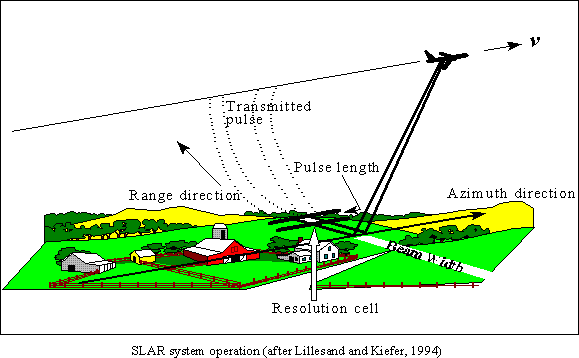
The pulse length dictates the spatial resolution in the direction of energy propagation (this is known as the "range direction"), while the antenna beam width determines the resolution cell in the flight, or "azimuth" direction.
Note that using a long pulse length, increases the possibility that the return signals from two adjacent features will be received simultaneously. If this is so, the two objects will be viewed as one feature.
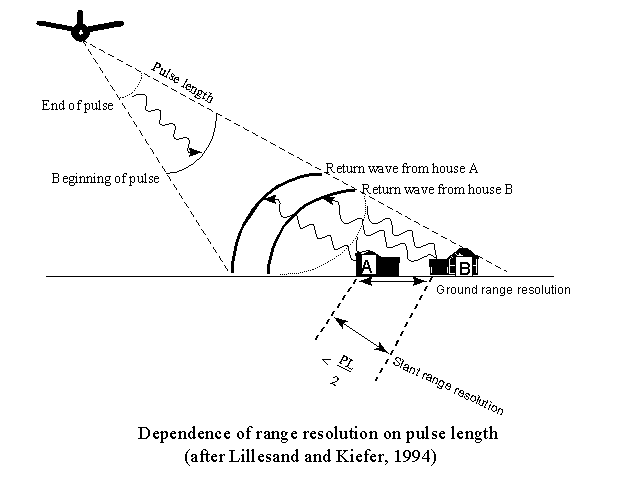
As seen in this diagram, if the distance between the two houses labeled A and B were greater than {Pulse Length ÷ 2} then
they would be discerned as two separate features. Since, in this figure the slant range distance is less than {Pulse Length ÷ 2},
the reflected signals are "blurred."
Slant range resolution does not vary with increasing distance from the aircraft, but ground range does.
Ground range resolution (Rr) is the horizontal expression of the slant range resolution (top) and is expressed mathematically as:
Rr=cT ÷ 2cos d , where:
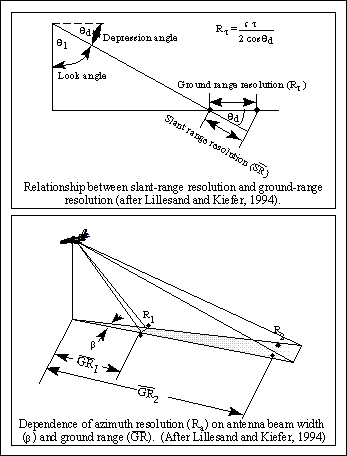
On examining the figure above and the preceding equation, it is clear that as the pulse duration decreases,
the ground resolution (horizontal distance) also decreases (meaning that the image can show greater spatial
detail).
There is an inverse relationship between the depression angle and ground range resolution: as d increases
from 0° to 90°, cos d decreases from 1 to 0. Therefore, as the depression angle increases the
ground resolution (horizontal distance) also increases, resulting in a decrease in spatial detail.
The azimuth resolution is the ground distance definition in the azimuth direction (i.e., the direction of the aircraft). The azimuth resolution, Ra, is at a 90° angle to the ground range, GR. Azimuth resolution may be expressed as:
Ra = GR * Beta, where:
The beam width of an instrument is in turn dependent on the wavelength transmitted and the antenna length. The relationship is shown by:
Beta=Wavelength ÷ Antenna Length
Since the antenna beam "fans out" with increasing distance from the transmitter, spatial detail decreases with increasing ground range (see figure, bottom). It is also advantageous to use the shortest possible wavelength, and the longest possible antenna (AL).
For any given wavelength, the antenna beam width may be controlled by either of the following methods:
Return to the Radar Mapping Home Page
Return to Hunter's Terrain Analysis Home Page