What is a datum?
Suppose you
have a pair of latitude-longitude coordinates, such as the following:
77° 2'
59.51'' W
38° 53' 20.95'' N
Do these
coordinates specify a single, definite point on earth?
The answer
really depends on how you interpret the question. A pair of
latitude-longitude coordinates, like the ones in the question above, do
uniquely identify a point on earth within the context of a particular
geographic coordinate system. But they don't identify a single point
absolutely—that is, if you change some of the settings of your geographic
coordinate system, the same pair of coordinates will mark a different place on
the earth.
Imagine two
geographic coordinate systems. Both are measured in degrees, so their
coordinate values are + or - 90 N/S and + or - 180 E/W. And both define the
How can
that be? A number of factors can make it happen. For example, it can happen if
the two geographic coordinate systems are associated with different spheroids.
(You saw an example of this in the very first exercise of the course, when you
looked at the coastline of
That sounds
a little abstract, but the basic idea isn't hard. Suppose you and I both make a
chocolate mousse, using the same ingredients and working in the same kitchen.
Nevertheless, our mousses come out tasting different. Why? Well, even though we
used the same ingredients, maybe we didn't follow exactly the same recipe. You
can think of a datum as something like the recipe for a geographic coordinate
system.
Components of a datum
In the
previous module, you learned that a geographic coordinate system has three
components: an angular unit of measure, a prime meridian, and a datum. The
first two are familiar to you, so now let's look at the third. Datums are an interesting subject, but for practical
purposes, you don't really need to know all the details that are presented
here—what matters most is knowing which datum you're working with, not exactly
how it's been defined.
The first
element of a datum is one we've already mentioned—the parameters of the
spheroid used to model the earth.
![]() Refresh your memory on the dimensions of a spheroid
Refresh your memory on the dimensions of a spheroid
A spheroid can be defined by the length of its semi-major
and semi-minor axes, or by the length of its semi-major axis and a flattening
value. (Flattening is the ratio of the semi-major to the semi-minor axis.)
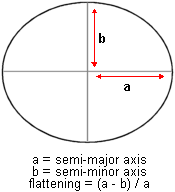
The dimensions of a
spheroid.
To get at
the second element, we have to consider a new idea. In the topic introduction,
you learned that the earth is best represented by a model called the geoid, but that this model has an irregular shape.
Therefore, coordinate systems are applied to the simpler model of a spheroid.
The problem is that actual measurements of location (whether made by ground
survey or satellite) conform to the geoid surface and
have to be mathematically recalculated to positions on the spheroid. This
process changes the measured positions of many points—sometimes by a few
meters, sometimes by hundreds of meters. It's an unavoidable compromise. To get
the mathematical convenience of a spheroid, you have to give up some positional
accuracy.
Which
points are affected? It depends. Different datums use
a different orientation of the spheroid to the geoid
to determine which parts of the world keep accurate coordinates on the
spheroid. For an area of interest, the surface of the spheroid can arbitrarily
be made to coincide with the surface of the geoid;
for this area, measurements can be accurately transferred from the geoid to the spheroid. The drawback is that in other areas
the geoid and the spheroid will not match up. In
these areas, point coordinates have to be adjusted (with loss of accuracy) when
they are moved from the geoid to the spheroid.
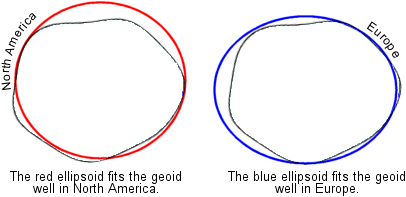
Left: the spheroid is
oriented to the geoid to preserve accurate
measurements for
So the
first element of a datum is the spheroid dimensions, and the second is the
orientation of the spheroid to the geoid. The third
element is the datum origin. This is a point whose latitude-longitude
coordinates on the spheroid are true to the geoid,
whose coordinates are not subject to adjustment, and to whose coordinates all
other points in the system are ultimately referred. The fourth element is an
azimuth value from the origin to a second point. As with the origin, this
azimuth measurement is preserved from the geoid to
the spheroid. It ultimately determines how the entire system of points is
spatially oriented with respect to the lines of latitude and longitude on the
spheroid.
This may
seem like a lot to digest, but you don't really need to remember it all (at
least not beyond the module exam). What you should remember is that changes to
the values of any datum parameters can result in changes to coordinate values
of points. It follows from this that if you have two different datums,
you also have two different geographic coordinate systems.
Once again,
the elements of a datum are:
·
a
spheroid
·
an
initial reference point, or origin
·
an
azimuth from the origin to a second point
·
the orientation of the spheroid to the geoid
(This is defined as the distance separating the geoid
and the spheroid at the origin, and it is usually zero.)
![]() Horizontal and vertical datums
Horizontal and vertical datums
Horizontal datums—the kind we've
been talking about here—are the reference values for a system of location
measurements. Vertical datums, by contrast, are the
reference values for a system of elevation measurements. The job of a vertical
datum is to define where zero elevation is—this is usually done by determining
mean sea level, a project that involves measuring tides over a cycle of many
years.
Local and earth-centered datums
Datums,
as described in the previous concept, are called local datums
because they preserve accurate point coordinates for a certain region, such as
![]() How are the coordinates of the origin determined?
How are the coordinates of the origin determined?
Latitude is determined by measuring angles to stars (in
particular, the North Star) and longitude is determined by comparing local time
to Greenwich time.
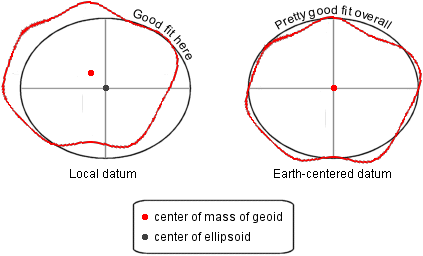
Left: in a local
datum, the spheroid matches the geoid closely in one
part of the world and is quite a bit off in others. The geoid's center of mass
does not align with the center of the spheroid. Right: in an earth-centered
datum, the spheroid matches the geoid pretty closely
all around the world, but nowhere perfectly-except at their centers.
Which type
of datum is better? It depends on your needs. An earth-centered datum is better
for mapping the world; a local datum is better for mapping a small piece of it.
Earth-centered datums, in particular WGS84, are
becoming a standard because they work equally well for everyone, but local datums will be around for a long time to come.
![]() Elements of an earth-centered datum
Elements of an earth-centered datum
The elements of an earth-centered datum are different from
those of a local datum (except that both specify an
spheroid). That's because the measurement technology is so different. Without
going into a description of satellite geodesy—which is complicated—it doesn't
really make sense to list the particulars of earth-centered datums.
To try to stuff it into a paragraph, we can say that the basic principle of
satellite geodesy is triangulation (same as earth-based surveying) and involves
locating points on earth in terms of how long it takes a ground station to
receive radio signals from different satellites. Consequently, the elements of
an earth-centered datum are things like satellite positions, the speed of
light, and synchronization values between satellite clocks and earth clocks.
Common datums
Local datums
North
American Datum of 1927 (NAD27)
Well-suited to the
European
Datum of 1950 (ED50)
Well-suited to the countries of continental
Well-suited to
Indian
Datum
Well-suited to
|
Datum |
Origin |
Origin coordinates |
Spheroid used |
|
NAD27 |
Meades Ranch, |
33° 13' 26.686" N |
Clarke 1866 |
|
ED50 |
|
52° 22' 51.45" N |
International 1924 |
|
|
|
35° 39' 17.51" N |
Bessel |
|
Indian |
|
24° 07' 11.26" N |
Everest |
Earth-centered
datums
World
Geodetic System of 1984 (WGS84)
The datum on which
Soviet
Geodetic System of 1990 (SGS90)
Similar to WGS84, this is the datum on which GLONASS coordinates are based.
(GLONASS, or the Global Navigation Satellite System, is
North
American Datum of 1983 (NAD83)
NAD83 is a correction of NAD27 coordinates that is based on both earth and
satellite measurements. Unlike NAD27, however, it is an earth-centered datum,
not a local datum. Its coordinates are very similar to WGS84 coordinates and
can be used interchangeably with them.
Datum transformations
As you saw
in the last topic, different datums lead to different
coordinate values for point locations. It follows that you'll run into problems
if you try to combine data sets that are based on different datums.
You've probably seen this for yourself in situations where two layers don't
line up like they should.
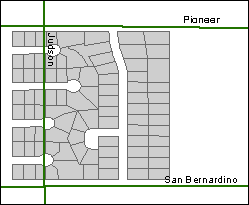
The streets and parcels
don't align because they are based on different datums.
The result is that a street runs through some parcels.
In this
topic, you'll see how problems like this can be resolved through datum
transformations. In the exercises, you'll get lots of practice applying datum
transformations in ArcMap. (You'll also get a better understanding of those
pesky warning messages that pop up whenver you add
layers based on different datums.)
In this
module, the terms "datum transformation" and "geographic
coordinate system transformation" are used interchangeably. Transforming a
datum also transforms the geographic coordinate system of which it is a part.