True direction and constant direction

The concept of direction is complicated by that fact that azimuth, or true direction, is one thing and constant direction is another. Let's compare these two ideas, using London and New Delhi as an example.

The azimuth from London to New Delhi is about 80 degrees. That value persists, however, only for a measurement made at London. As you follow that great circle arc toward New Delhi, the azimuth value changes with respect to your local meridian.

Therefore, as you follow an oblique arc, the angle at which you intercept meridians changes with your latitude. The only great circles of constant azimuth are the equator and the meridians.

In the graphic below, a line of true direction from London to New Delhi is shown in red. As the local meridian changes along the arc, so does the azimuth value.

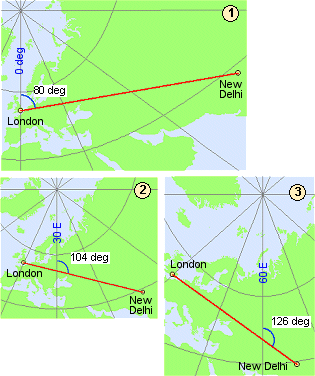
In 1), the azimuth is measured with respect to the prime meridian. In 2), the projection is recentered and the azimuth is measured with respect to the 30°E meridian. In 3), the projection is again recentered, and the azimuth is measured with respect to the 60°E meridian. The arc of true direction doesn't change; all that changes is the angle at which it intercepts each meridian. (The projection used here is the Gnomonic, in which all great circles project as straight lines.)

For navigators, a line of true direction is a headache—it's the shortest way from A to B, but you have to keep changing your compass bearings to stay on course.

A line of constant direction (also called a rhumb line or loxodrome) is an alternative way to get from A to B. It's not a great circle arc, so it's not the shortest route, but it's easier to navigate because it crosses every meridian at the same angle. You just follow a constant compass heading—say, 45 degrees—and eventually you get to your destination.

The most famous constant direction map is the Mercator. On it, every rhumb line is projected as a straight line.

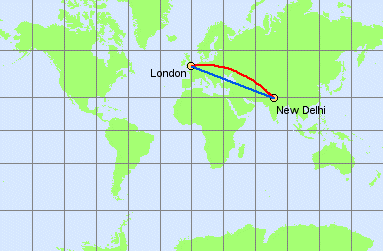
On a Mercator projection, all straight lines, like the blue line from London to New Delhi, are lines of constant direction. A bearing of 111° (measured clockwise from north) takes you from London to New Delhi. The azimuthal line is shown in red.

On an azimuthal map, lines of constant direction are projected as curves.

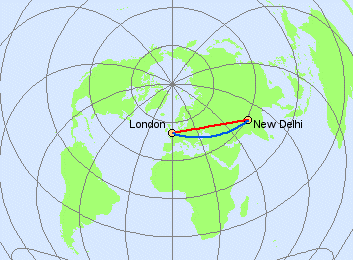
A Gnomonic projection. The red line is azimuth; the blue line is constant direction. The true distance from London to New Delhi is about 6,730 kilometers. Along the rhumb line, it is about 7,015 kilometers.