The earth's shape is a spheroid

Although the earth's shape is technically an ellipsoid, its major and minor axes do not vary greatly. In fact, its shape is so close to a sphere that it is often called a spheroid rather than an ellipsoid.

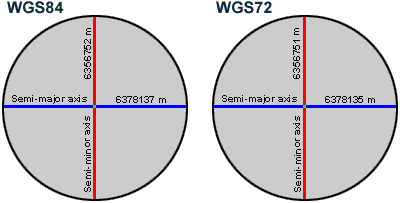
A spheroid is simply an ellipsoid that approximates a sphere. These examples are two common world spheroids used today with their values rounded to the nearest meter. For each spheroid, the difference between its major axis and its minor axis is less than 0.34 percent.

The terms "spheroid" and "ellipsoid" are often used interchangeably and have caused confusion for many GIS users. Most map projection authorities consider both terms equally correct. Specific definitions for exactly what a spheroid is can vary, but the two most common definitions for a spheroid are:

1. An ellipsoid that approximates the shape of a sphere

2. An ellipsoid created by rotating an ellipse about either its major axis (called a prolate spheroid) or its minor axis (called an oblate spheroid)

The second definition is generally considered a more precise geometric definition because it doesn't involve any subjectivity. Using this definition, the earth's shape would be described as an oblate spheroid. To most people, however, the first spheroid definition better describes the earth's shape, so that will be the definition used in this course.

Defining ellipticity

The degree of ellipticity, or flattening, of an ellipse, ellipsoid, or spheroid can be expressed as a fraction or decimal measuring the difference in the length of the two axes. For example, if you assign two axes to a circle, and measure both of them, the resulting difference will be 0. A circle's ellipticity is therefore 0. As an ellipse becomes more elongated its ellipticity increases. Eventually, it approaches the shape of a line, which has an ellipticity of 1.

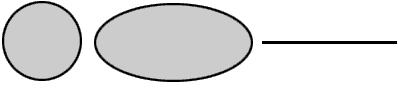
A circle has an ellipticity equal to 0 because the length of both axes is the same. The example ellipse above has an ellipticity of .5 because the major axis is twice as long as the minor axis. A line has an ellipticity of 1 because it has length but no height.

Large elliptical values describe narrow ellipses or ellipsoids and small elliptical values represent almost circular ellipses or spheroids. Earth's ellipticity is approximately 0.003353 because it bulges slightly at the equator and is flattened at the poles. While this difference doesn't seem like much, it can greatly affect large-scale maps.

Why do we need different spheroids?

Now you know that the earth is a spheroid (which is another word for ellipsoid). As you may have suspected, however, it is not a perfect spheroid. The earth's surface is not perfectly symmetrical, so the semi-major and semi-minor axes that fit one geographical region do not necessarily fit another one.

Satellite technology has revealed several elliptical deviations. For one thing, the most southerly point on the minor axis (the South Pole) is closer to the major axis (the equator) than is the most northerly point on the minor axis (the North Pole). In addition, the earth's spheroid deviates slightly for different regions of the earth.

Many different spheroids are used throughout the world to account for these deviations. For example, the International 1924 and the Bessel 1841 spheroids are used in Europe while in North America the GRS80 spheroid is the most common. Ignoring deviations and using the same spheroid for all locations on the earth could lead to errors of several meters, or in extreme cases hundreds of meters, in measurements on a regional scale.

Because of improvements in technology, refinements in measurements, or for political reasons, you may see different spheroids used for the same geographic area. For example, until recently, the Clarke 1866 spheroid was the most commonly used spheroid for North America. Today, the GRS80 spheroid is replacing Clarke 1866 in most geographic databases. However, just because a spatial database covers North America, you cannot assume it uses the GRS80 spheroid. Many North American databases have not yet been converted from Clarke 1866.

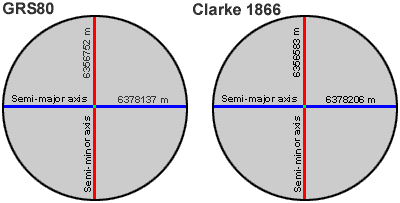
Spheroids created using satellite information, such as GRS80, are starting to replace traditional ground-measured spheroids, such as Clarke 1866. In this example, measurements for both spheroids have been rounded to the nearest meter.

As technology improves, more spheroids of higher local accuracy will be developed. Remember that changing spheroids changes the location values for the features you are mapping. Because of the complexity of changing spheroids, ground-measured spheroids will remain in use for several years.

When to use a sphere

Although a spheroid best represents the earth's shape, the earth is sometimes treated as a sphere to make mathematical calculations easier.

You can use a variety of methods to define a sphere that approximates the earth's shape. For instance, you could base your sphere on either the major axis or the minor axis of the earth (as defined by a particular spheroid). The most commonly accepted method, however, is to create a sphere that has the same surface area as the spheroid. Such a sphere is called an authalic sphere. Although there are discrepancies between authalic spheres, the most common authalic sphere diameter used is 12,741.994 kilometers or 7,912.778 miles.

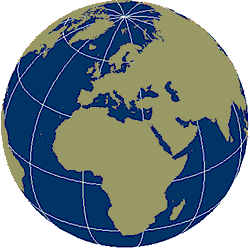
While difference between the semi-major and semi-minor axes must be considered in regional applications, for most world maps the difference can be ignored and the world can be treated as a sphere. In fact, the difference is so small that for this graphic it would be undetectable.

If your mapping scales are smaller than 1:5,000,000 (small-scale maps), you can use an authalic sphere to define the earth's shape. To give you some perspective, a 1:5,000,000 scale map of the coterminous United States would be approximately 122cm (48") wide. At this scale, the difference between a sphere and a spheroid is not significant. If your applications use scales that are larger than this, you may need to choose a spheroid.

Unless you specify a sphere for your application, ESRI products use an authalic sphere with a diameter of 12,741.994 kilometers or 7,912.778 miles.