Lab 13

Statistical Models

This lab exercise is slightly different from the other ones involving . Remember that is a full-fledged statistics package for professional applications and professionals often see their subject matter differently from how it is taught in introductory courses. Correlation and regression are seen by them as part of a larger concept of statistical models and we will have to cover this concept before we can embark on applying routines. And the analysis of variance (ANOVA) that we discussed in the lecture as part of sample-based procedures, turns out to be a special kind of statistical model. Models and hypotheses succeed in simplifying complex situations by ignoring information outside their frame and by accurate generalization within it.

Step 1 Deterministic models

Mathematical or deterministic models are used to describe regular law-like behavior. In fundamental research in the physical sciences, deterministic models are often adequate. Statistical variability is so small that it can be ignored.

> x = 1:5

> y = 0.5 * 9.8 * x^2

> plot(y~x, xlab = “Time (s) “, ylab = “Distance fallen (m) “)

> lines (spline(x,y)) # pass a smooth curve through the points

Step 2 Statistical models

Statistical models rely on probabilistic forms of description that have wide application over all areas of science. They often consist of a deterministic component as well as a random component that attempts to account for variation that is not accounted for by a law-like property. In engineering terms, the deterministic part is called a signal and the random part noise. Typically, we assume that the elements of the noise component are uncorrelated. Take the roller.txt table for instance. Here, different weights of roller were rolled over different parts of a lawn, and the depression noted. We might expect depression to be proportional to roller weight – the signal part. The variation exhibited in the values for depression/weight makes it clear that this is not the whole story. We therefore model deviations from the line as random noise:

depression = b * weight + noise

Here b is a constant, which we do not know but can try to estimate. The noise is different for each different part of the lawn. If there were no noise, all the points would lie exactly on a line.

> roller = read.table(“roller.txt”, header=T)

> roller

> plot(depression ~ weight, data=roller, xlab=”Weight of roller (t) “, ylab=”Depression (mm) “)

> abline(0,2.25) # a slope of 2.25 looks about right

Many models have the form

observed value = model prediction + statistical error,

or mathematically:

Y = m + e

Using the mathematical idea of expected value, it is usual to define m = E(Y ). The error term e is assumed to be independent and normally distributed.

After fitting a line through the lawn roller data, we can predict the depression that would result for a given weight. The accuracy of the prediction depends upon the amount of noise.

Step 3 Model formulae

’s modeling functions use formulae to describe the role of variables in models. A large part of the analyst’s task is to find the model formula that will be effective for the task in hand. For example, the following model statement with formula depression ~ weight, fits a line to the roller data:

> lm(depression ~ weight, data =roller) # prints out summary information

The lm() function stands for linear model. Note that this fits a model that has an intercept term y_i = a + bx_i. The nonrandom part of the equation describes y_i as lying on a straight line. The slope of the line (the regression coefficient) is b, the increase per unit change in x. The line intersects the y-axis at the intercept a. For a model that omits the intercept term, specify

> lm(depression ~ -1 + weight, data = roller)

The parameters a and b can be estimated using the method of least squares.

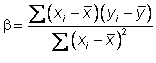
The argument to lm() is a model formula, in which the tilde symbol (~) should be read as “described by”. This has been seen several times earlier, both in connection with boxplots and stripcharts and with the t and Wilcoxon tests. 

The lm() function handles much more complicated models than simple linear regression. There can be many other things besides a dependent and a descriptive variable in a model formula. In its raw form, the output of lm() is very brief. All you see is the estimated intercept a and the estimated slope b.

Step 4 Model objects

The result of lm() is a model object. This is a distinct concept of . Where other statistical software packages focus on generating printed output, you get instead the result of a model fit encapsulated in an object from which the desired quantities can be obtained using extractor functions. An lm object does in fact contain much more information than you see when it is printed. A basic extractor function is summary():

> summary(lm(depression~weight, data=roller))

The following is a dissection of the output.

Call:

lm(formula = depression ~ weight, data = roller)

Like in t.test(), etc., the output starts with something that is essentially a repeat of the function call. This is not very interesting when one has just given it as a command to , but it is useful if the result is saved in a variable that is printed later.

Residuals:

Min 1Q Median 3Q Max

-8.180 -5.580 -1.346 5.920 8.020

This gives a superficial view of the distribution of the residuals, which may be used to check distributional assumptions. The average of the residuals is zero by definition, so the median should not be far from zero and the minimum and the maximum should be roughly equal in absolute value.

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) -2.0871 4.7543 -0.439 0.67227

weight 2.6667 0.7002 3.808 0.00518 **

---

Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1

Here we see the regression coefficient and the intercept again, but this time with accompanying standard errors, t tests, and p –values. The symbols to the right are graphical indicators of the level of significance. The line below the table shows the definition of these indicators; one star means 0.01 < p < 0.05.

Residual standard error: 6.735 on 8 degrees of freedom

This is the residual variation, an expression of the variation of the observation around the regression line, estimating the model parameter s.

Multiple R-Squared: 0.6445, Adjusted R-squared: 0.6001

The first term above is R², which in simple linear regression may be recognized as the squared Pearson correlation coefficient. The other one is the adjusted R²; if you multiply it by 100%, it can be interpreted as “% variance reduction”.

F-statistic: 14.5 on 1 and 8 DF, p-value: 0.005175

This is an F test for the hypothesis that the regression coefficient is zero. This test is not really interesting in a simple linear regression analysis since it just duplicates information already given – it becomes more interesting when there is more than one explanatory variable. Notice that it gives the exact same result as the t test for a zero slope. In fact, the F test is identical to the square of the t test: 14.5 = (3.808)². This is true in any model with one degree of freedom.

Now we don’t need to guess the regression line anymore as it fits best through the roller measurements. In

> plot(depression ~ weight, data=roller, xlab=”Weight of roller (t) “, ylab=”Depression (mm) “)

> abline(lm(depression ~ weight, data=roller))

We now use the content of the lm object to define a line based on the intercept (a) and slope (b) (hence the name of the function abline()). It can be used with scalar values as in abline(1.1, 0.022), but conveniently it can also extract the information from the linear model fitted to data with lm().

Step 5 Residual and fitted values

We have seen how summary() can be used to extract information about the results of a regression analysis. Two further extraction functions are fitted() and resid(). They are used as follows. For convenience, we first store the value returned by lm() under the name lm.roller, but you could of course use any other name.

> lm.roller = lm(depression ~ weight, data=roller)

> fitted(lm.roller)

> resid(lm.roller)

The function fitted() returns fitted values – the y-values that you would expect for given x-values according to the best-fitting straight line: in the present case -2.087 + 2.66 weight. The residuals shown by resid() is the difference between this and the observed depression.

Step 6 Prediction and confidence intervals

Fitted lines are often presented with uncertainty bands around them. There are two kinds of bands, often referred to as the “narrow” and “wide” limits. The narrow bands, confidence bands, reflect the uncertainty about the line itself. If there are many observations, the bands will be quite narrow, reflecting a well-determined line.

The wide bands, prediction bands, include uncertainty about future observations. The bands should capture the majority of observed points and will not collapse to a line as the number of observations increases. Rather, the limits approach the true line ±2 standard deviations (for 95% limits).

Predicted values, with or without prediction and confidence bands, may be extracted with the function predict(). With no arguments, it gives the fitted values:

> predict(lm.roller)

If you add interval=”confidence” or “interval=”prediction” then you get the vector of predicted values augmented with limits. The arguments can be abbreviated:

> predict(lm.roller, int=”c”)

> predict(lm.roller, int=”p”)

fit is the expected values, here identical to the fitted values. lwr and upr (lower/upper) are the confidence limits for the expected values, respectively, the prediction limits for depression with these limits of weight.

Step 7 Correlation

A correlation coefficient is a measure of association between two random variables. It ranges from -1 to +1, where the extremes indicate perfect correlation and 0 means no correlation. The function cor() can be used to compute the correlation between two or more vectors.

> cor(roller)

Of course, this is more interesting when the data frame contains more than two vectors. However, the above calculations give no indication of whether the correlation is significantly different from zero. To that end, you need cor.test(). It works simply by specifying the two variables:

> cor.test(roller$depression, roller$weight)

Notice that it is the same p-value as in the regression analysis and also as that based on the ANOVA table for the regression model that will be described in step 8.

As with the one- and two-sample problems, you may be interested in nonparametric variants. These have the advantage of not depending on the normal distribution. The main disadvantage is that its interpretation is not quite clear. Unlike group comparisons where there is essential one function per named test, correlation tests are all grouped into cor.test(). There is no special spearman.test() function. Instead, the test is considered one of several possibilities for testing correlations and is therefore specified via an option to cor.test():

> cor.test(roller$depression, roller$weight, method=”spearman”)

Step 8 ANOVA

Simple analysis of variance can be performed in using the function lm(). For more elaborate analyses, there is anova(). We calculate a model object using lm() and extract the analysis of variance table with anova().

> anova(lm(depression~weight, data =roller)

In the lecture, I referred to “between groups” and “within groups” sums of squares. uses a slightly different labeling. Variation between groups is labeled by the name of the grouping factor (here weight) and variation within groups is labeled Residual. ANOVA tables can be used for a wide range of statistical models, and it is convenient to use a format that is less linked to the particular problem of comparing groups.

With this, we are ready to turn you loose on trying yourself with statistical modeling. Here are your tasks for today’s lab. As before, record all your answers to the above six questions and send them in an ASCII email message to Jing Li.

1 Use read.csv() to import the homes.txt table that we discussed in the lecture and calculate the ANOVA F test statistic. Do the four neighborhoods represent one or more housing markets?

2 Read the snow.txt table that we discussed in the lecture and determine the correlation coefficient r. What is the t test statistic or the p value indicating the significance of the result?

3 What is the regression line equation that best fits the snowfall data?

4 How much of the variation (in %) is explained by the equation that you calculated in Q3?