Lab 10

Probability and Distributions

 

We are still following the sequence of lectures. All geographic explanation has to make sure that there really is something driving the particular spatial pattern that we observe and that our empirical data is not just the result of pure chance. While there are many analytical methods that try to explain a particular spatial pattern (the discipline or domain of spatial analysis), we will here in this lab and in this course in general, restrict ourselves to methods of traditional statistics. The emphasis is on discussing the relationship between samples and populations. By now, you should be familiar with the general way of how [R logo] works. If you have problems with accessing files from with [R logo], assigning values to variables, indexing vectors and tables, then you are advised to revisit the previous two lab exercises.

Estimated time to complete this lab: 100 minutes

 

Studying spatial patterns found on the physical and cultural landscape is a central concern of geographers. They seek to develop descriptions and explanations of existing patterns and to understand the processes that create these distributions. In some cases, they attempt to predict future occurrences of geographic patterns. In the previous labs, the emphasis was on ways to describe or summarize spatial data. Much of the remainder of this course involves methods used for exploring relationships between spatial data for understanding the nature of the processes that led to their existence. The concept of probability occupies a central position here.

Typically, geographic processes are too complex to be deterministic, that is complete describable and understandable. Because of uncertainty in human behavior and decision making, virtually no cultural process and very few physical processes (because which physical process is completely undisturbed by human influences these days?) are completely deterministic. We call these probabilistic processes, which is the realm of statistics. It is this uncertainty that characterizes statistical analysis, and our goal is to make as much sense of data as possible, while acknowledging that our understanding is imperfect.

Since most geographic processes have some degree of uncertainty, geographers need to understand and use probability for solving problems. For example, every location on the earth’s surface receives a variable amount of precipitation. These data can be recorded over time and space, and precipitation patterns can be summarized using calculations such as mean and standard deviation. However, since precipitation is the result of complex atmospheric processes, its prediction can only be stated in terms of probability, not certainty. The exact amount of snowfall next January cannot be determined until after the fact.

The study of probability focuses on the occurrence of an event, which can result in one of several outcomes. And if we don’t have any additional prior knowledge, then we have to assume that all outcomes are equally likely, in other words, the outcome is random. In [R logo], we simulate these situations with the sample function. If you want to pick five numbers at random from a set of 1:40, then you write

> sample(1:40,5)

The first argument (x) is a vector of values to be sampled and the second (size) is the sample size. Actually, sample(40,5) would suffice since a single number is interpreted to represent the length of a sequence of integers. (There are a lot of such in-built assumptions in [R logo]; the challenge lies in learning to understand them as shortcuts to an otherwise longer but much more logical structure).

 

Step 1         Start [R logo] and change your working directory to U:/GTECH201/R (or another folder of your choice)

 

Step 2         Create a random sample

> sample(1:40,5)

Notice that the default behavior of sample is sampling without replacement. Thus, the samples will not contain the same number twice, and size can obviously not be bigger than the length of the vector to be sampled. To simulate 10 coin tosses, we could write

> sample(c("H", "T"), 10, replace=T)

In fair coin-tossing, the probability of heads should equal the probability of tails, but this symmetry is not always realistic or desirable. We may be interested in simulating the outcome of a series of surgical procedures, whose overall success rate is 90%. We do this in [R logo] by adding the prob argument to the sample function:

> sample(c("succ", "fail"), 10, replace=T, prob=c(0.9, 0.1))

Collecting sample data of outcomes from such experiments (when the sample is only a portion of the population) and then calculating the probabilities of different outcomes is the basis for statistical inference.

Probability can be thought of as relative frequency – the ratio between the absolute frequency for a particular outcome and the frequency of all outcomes. For example, by keeping records of wet days and dry days over a 100-day period, absolute frequencies of precipitation can be determined and relative probabilities calculated. If 62 days are categorized as dry days, and 38 as wet, then the probability of a wet day occurring is P(W) = number of wet days divided by total number of days = .38. The complement, the number of dry days is the difference between .38 and 1, which in this case is .62.

If two events are independent from each other, then the probability for both of them occurring is the multiplication of one probability with the other one. Since we are dealing with 0 ≤ prob ≤ 1, the resulting combined probability is usually a much smaller number. If we are satisfied with either one of these, then you can safely add the individual probabilities.

 

Step 3         Arithmetic of probabilities

Load into [R logo] table immigration.txt, which lists the number of immigrants from selected countries to the US census regions in 1992:

> immigration=read.table("immigration.txt", header=T, row.names=1)

Please observe the last parameter, which allows us to treat rows and columns interchangeably as variables. We can now query the table horizontally by origin of the immigrants or vertically by census region destination. Display the contents of the new data frame and study the categories. Some are mutually exclusive, for example, you can be born in only one country. Others are not mutually exclusive, for example, a single immigrant could come from Mexico and settle in the Northeast. Using the explanation of probability arithmetic at the end of step 2,

Question 1a   Calculate the probability that an immigrant is from Vietnam or from the Philippines.

       b   Calculate the probability that an immigrant is from Vietnam, is settling in the West, or both. Beware: these two categories are not mutually exclusive, so have to deal with additions and multiplications.

Step 3         Calculating binomial probabilities

The probability of outcomes in certain problems follows consistent or typical patterns. They are called probability distributions. We will look at three distributions in particular: binomial, Poisson, and normal.

The binomial distribution is a discrete probability associated with events that have only two possible outcomes: yes/no, dry days wet days, employed/unemployed, etc. The binomial distribution is especially useful in examining probabilities from multiple events, such as the flooding history of a river. For example, the probability of a river in Bangladesh reaching flood stage during a given year may be .40. Thus, on average, flooding occurs in four years out of ten. The probability for a given outcome P(X) = n! pX qn-X / X!(n-X)! Recall from the lecture that the exclamation mark in n! is a mathematical symbol standing for n factorial, which is shorthand for n times n-1 times n-2 down to 1, e.g., 5! = 5 * 4 * 3 * 2 * 1 = 120. We calculate the factorial in [R logo] using the prod() function, e.g., prod(5:1) for 5!. Finally, to raise x to the power of n (xn), you write x ** n.

Question 2 Calculate the probability that we will observe 15 flooding years out of 30.

Step 4         Calculating Poisson probabilities

Some problems in geography involve the study of events that occur repeatedly and randomly over either time or space. For example, at certain spatial scales, multiple events of weather-related phenomena, such as thunderstorms, tornadoes, and hurricanes, may occur with little spatial predictability. In instances, where events occur repeatedly and at random, the Poisson probability distribution can be used. The application areas for the binomial and the Poisson distributions are very similar. The main differences are that
(a) we are not looking anymore at merely binary outcomes. Rather than asking whether there will be a flood year, we ask more specifically how many flood per year
(b) we use the summary statistics of our historical data, in particular the mean frequency of occurrence.

The equation behind the Poisson distribution is P(X) = lX /( el(X!)), where l is the mean frequency, which we so far described with x bar or .

Question 3   Read the table hail.txt and determine the probabilities for zero, one, two, three, four, or 5+ hail storms per year in the Canadian province of Manitoba using the Poisson formula. Then plot a histogram of the observed frequency distribution and copy it to your web page with Lab10 submissions.

We will be revisiting the Poisson distribution when we talk about spatial statistics in particular.

 

Step 5         Review of normal probabilities

The most generally applied probability distribution is the normal distribution. When a set of geographic data is normally distributed, many useful conclusions can be drawn, and various properties of the data can be assumed. The normal distribution provides the basis for sampling theory and statistical inference.

The most striking characteristic of the normal curve is its symmetry; the lower (left-hand) and upper (right-hand) ends of the frequency distribution are balanced.

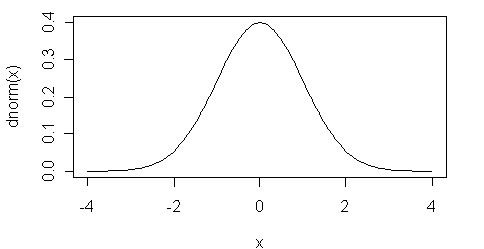
The central value of the data represents the peak or most frequently occurring value. The way in which areas are distributed under the normal curve provides the basis for making probability estimates. The total area under the normal curve represents 100% of the outcomes. Given the symmetric form of the normal curve, it is clear that 50% of the values are greater than the mean and that a value taken from a normal distribution has a .50 probability of falling above the mean. However, to determine percentages for other intervals, integral calculus is needed (No worries: [R logo] does this for you). Which points out the main difference between the binomial and Poisson distribution discussed before and the normal distribution here: the normal distribution models continuous data. Because there are infinitely many numbers infinitely close, the probability of any particular value will be zero, so there is no such thing as a point probability as for discrete distributions. Instead, we have the concept of density: this is the infinitesimal probability of hitting s small region around x, divided by the size of the region.

While all normal curves have the characteristic bell shape, the actual form is determined by the mean and standard deviation of our data set:

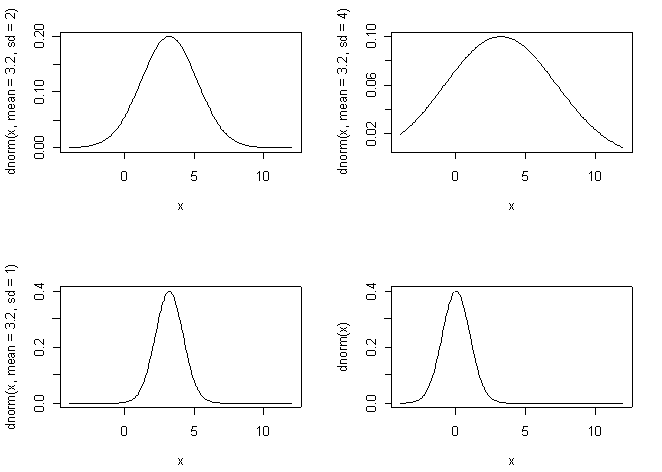
To compare datasets with different means and standard variations, we often standardize the normal curve to a uniform distribution, or standardized scale. On a standardized scale, each observation is assigned a standard score or Z value, which indicates how many standard deviations separate a particular measurement from the mean of the distribution. Standard scores can be either positive or negative. For units of data greater than the mean, the corresponding standard score is positive; a score of zero corresponds to the value being exactly equal to the mean of the distribution.

Step 6         The built-in distribution in [R logo]

Generations of students before you, had to work with look-up tables to make use of standard distributions. [R logo] has more than 20 built-in distributions, and for each of these, there are four fundamental items that can be calculated:

  • Density or point probability
  • Cumulated probability; distribution function
  • Quantiles, and
  • Pseudo random numbers

The naming scheme is very consequent; for the normal distribution, for instance, the four respective functions are called dnorm, pnorm, qnorm, and rnorm.

As mentioned above, the density for a continuous distribution is a measure of the relative probability of getting a value close to x. The probability of getting a value in a particular interval is the area under the corresponding part of the curve. For discrete distributions, the term “density” is used for the point probability – the probability of getting exactly the value x. An example for the use of ofthe density function is

> x = seq(-4, 4, 0.1)

> plot(x, dnorm(x), type="l")

For discrete distributions, where variables can take on only distinct values, it is preferable to draw a pin diagram, here for the binomial distribution with n=50 and p=.033.

> x = 0:50

> plot(x, dbinom(x, size=50, prob=.33), type="h")

Notice that for the normal distribution, we could have given parameters similar to size and probability for the binomial distribution. The arguments in case of the normal distribution would have been figures for the mean and the standard distribution. These can be omitted if we are happy with the default values of 0 for mean and 1 for standard distribution respectively.

The cumulative distribution function describes the probability of hitting x or less in a given distribution. The corresponding [R logo] functions begin with a ‘p’ by convention. As an example, consider a population of raisin buns for which there is an average of 3 raisins per bun. We observe the following distribution:

> dpois(x=0:4, lambda=3)

[1] 0.04978707    0.14936121    0.22404181    0.22404181    0.16803136

The cumulative probabilities can then be calculated with

> ppois(q=0:4, lambda=3)

Telling us, for example that the cumulative probability of observing 2 or fewer raisins in a bun is .4232.

With this, we are ready for the next lab question, where we revisit the precipitation dataset for BWI airport from the last lab session. This data is approximately normally distributed over 54 years with a mean of 41.34 inches and a standard deviation of  7.85 inches. Read precip.txt, extract the data for BWI, and determine

Question 4 What is the probability of annual precipitation at BWI to exceed 50 inches? Note your answer in your Lab10 web page.

The quantile function is the inverse of the cumulative distribution function. The p-quantile is the value with the property that there is probability p of getting a value less than or equal to it. The median is by definition the 50% quantile. Theoretical quantiles are commonly used for the calculation of confidence intervals, which we will cover in depth in the next lab session.

Finally, there [R logo] has built-in random number generators for each of the 20+ distributions. The use of the functions that generate random numbers is straightforward. The first argument specifies the number of random numbers to compute, and the subsequent arguments are similar to those for other functions related to the same distribution. For instance

> rnorm(10)

> rnorm(10)          # yes, the same function call again; you can see that the numbers are now completely different

> rnorm(10, mean=7, sd=5)

> rbinom(10, size=20, prob=.5)

 

Step 7         Understanding the effect of sample size

In preparation for the next lab session, let’s look at the effect of sample size on the shape of density distribution functions.

Question 5   Use the parameter mfrow to par() to set up the layout for a 3 by 4 array of plots. In the top 4 panels, show normal probability plots for 4 separate random samples of size 10, all from the normal distribution. In the middle four panels, display plots for samples of size 100. In the bottom 4 panels display plots for samples of size 1,000. Comment on how the appearance of the plots changes as the sample size changes.

Question 6   The function runif() generates a sample from a uniform distribution (see last paragraph in step 5). Try x = runif(10) and print the resulting numbers to your screen. Then repeat Q5 above, but taking samples from the uniform distribution rather than from the normal distribution. What shapes do the plots follow?

Rename your web page lab10.answers.html and set a link to this page from your home page. Then send an email to Jing Li announcing your lab submission and providing him with the URL to your lab answers.