The earth's shape is an ellipsoid
As the
centuries passed, scientists and explorers began to realize that the earth was
not a perfect sphere.
British
scientists, led by Isaac Newton, theorized that the centrifugal force from the earth's
rotation would force the earth to "spread out" from east to west as
it rotated about its axis. The French, using their own local measurements,
believed the earth to be squished at the equator and bulging at the poles. In
1753, this debate was resolved when a French survey expedition took
measurements at the equator in
Just as a sphere is based on a circle, an ellipsoid is based on an ellipse. By rotating an ellipse about one of its axes, an ellipsoid of rotation is created. It is this type of ellipsoid that most closely approximates the earth's shape. To be more precise, the earth rotates about its shortest axis, or minor axis, and is therefore described as an oblate ellipsoid.

The earth is not a perfect sphere but an oblate ellipsoid. If it rotated about its major (longer) axis, it would be described as a prolate ellipsoid.
Ellipses and ellipsoids
How to
make an ellipse
No one knows for sure when the ellipse was discovered, but in 350

The ellipse is one of the
many conic section shapes, such as a line, circle, parabola, or hyperbola.
An ellipse is basically a curve with a simple formula. Create a straight line (X in the graphic below) connecting two fixed points (A and B), called foci. Next, create another straight line (Y) that begins at one of the foci and ends at a new point (C) that is not on the first line (X). Move the end point (C) while keeping the summed distance of the two lines (X+Y and Y) the same until you return to the starting point and you will create an ellipse.
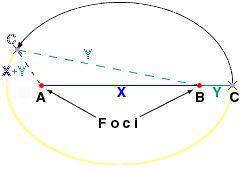
Moving point C while keeping the summed length of lines X+Y and Y constant creates an ellipse.
For nearly
two thousand years, the ellipse had no known application in nature, a situation
most early astronomers and alchemists had difficulty accepting. Early in the
seventeenth century, German astronomer and philosopher, Johannes Kepler, seeking an explanation for the unusual orbits of
the planets around the sun, discovered that the ellipse described the orbits
perfectly. Kepler had his solution and the ellipse
had its first known application. Little did Kepler
know that the shapes of the planets themselves are best described as
ellipsoids—a three-dimensional representation of an ellipse.
Making
an ellipsoid
Drawing a line through an ellipse's two foci and then another line
perpendicular to and bisecting this line creates two axes, a major axis and a
minor axis. Rotating an ellipse about either axis creates a special type of
ellipsoid called an ellipsoid of rotation.
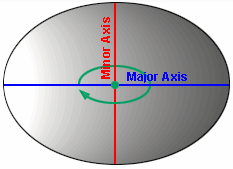
Spinning an ellipse about its minor axis creates an oblate ellipsoid while spinning an ellipse about its major axis creates a prolate ellipsoid.
Ellipsoids of rotation are defined using two axes but ellipsoids are actually mathematically defined using three axes. When you rotate the ellipse about one of its axes, as in an ellipsoid of rotation, two of the axes are equal.
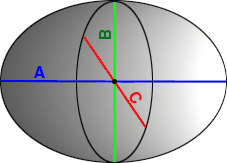
Not all ellipsoids are ellipsoids of rotation. Mathematically an ellipsoid is triaxial or defined using three axes (A,B,C).
Ellipsoids are not usually measured with major and minor axes but rather with semi-axes. A semi-axis is half of an axis.
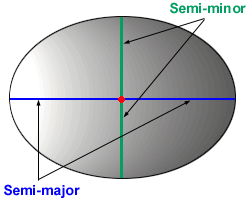
When you examine the parameters for any ellipsoid used to describe the earth, its semi-major and semi-minor axes are given.